- Download:
- MP3 Audio17 MB
- MPEG-4 AAC Audio13 MB
Aristoteles – Der Logiker – Folge 7
Heute geht es um Logik – I f*cking love logic! Ich lege den Satz vom ausgeschlossenen Dritten dar und was er bedeutet. Anschließend quadrieren wir die Logik indem ich mit euch im Detail Kontradiktionen, konträre Gegenteile und den ganzen Kladderadatsch durchgehe. Wie gewohnt habt ihr die Wahl zwischen Video, Podcast oder Text.
Wie kann ein Quadrat logisch sein?
So langsam nähern wir uns der Logik von Aristoteles. Und das machen wir über das sogenannte logische Quadrat. Logisches Quadrat? Das klingt für mich ein bisschen wie ein Spiel in Squid Game. Allerdings steht der Name „logisches Quadrat“ für mehrere logisch-semantische Beziehungen und der Name stammt gar nicht von Aristoteles. Wer genau erstmals auf die quadratische Darstellung kam, ist unklar. Die älteste uns bekannte Erwähnung stammt von Apuleius von Madauros aus dem 2. Jahrhundert nach Christus, also gut 400 Jahre nach Aris Tod.
Aber bevor ich länger kryptisch von irgendwelchen Quadraten und wer sie erfunden hat spreche, als wäre ich in einem Tarantino-Film, sollte ich erst einmal klarmachen, worum es wirklich geht. Aristoteles beschreibt in der De Interpretatione zwei semantische Beziehungen, die wir dringend brauchen, bevor wir anfangen können, logische Schlüsse zu fällen: konträr und kontradiktorisch.
Nein, ich merke gerade, ich war zu voreilig – ganz wie die BBC, als sie bereits 2016 die 100 besten Filme des 21. Jahrhunderts kürte. Hmmm. Daher muss ich noch einen Schritt zurückgehen. Denn bevor wir uns mit Kontradiktionen und konträren Gegenteilen beschäftigen, müssen wir mit den beiden grundlegendsten Begriffen der Logik anfangen: Ich spreche von den kleinen Begriffen „wahr“ und „falsch“.
Der Satz vom ausgeschlossenen Dritten
Ari formuliert in De Interpretatione einen der wichtigsten Sätze der Logik überhaupt. Wichtiger noch als „Aus großer Macht folgt große Verantwortung“ oder „Möge die Macht mit dir sein“: Den Satz vom ausgeschlossenen Dritten. Demnach kann etwas nur wahr oder falsch sein. Aber nichts dazwischen und nicht beides.
Wenn ihr euch für Politik interessiert, euch schon mal mit euren Eltern gestritten habt oder von irgendjemanden den Satz gehört habt: „Man muss Butter unter Nutella schmieren“, dann habt ihr eben bestimmt zischend die Luft zwischen den Zähnen eingesogen und ich werde gleich weiter auf Probleme und Einschränkungen des Satzes vom ausgeschlossenen Dritten eingehen. Aber folgen wir zunächst einmal Aristoteles, bevor wir anfangen ihn zu kritisieren und schauen was er macht. Denn der Satz vom ausgeschlossenen Dritten ist keine ganz dumme Idee.
In der formalen Logik können wir das durch eine einfache Formalisierung verdeutlichen. Nehmen wir dafür den Satz: „Ein Film der sowohl lustige als auch traurige Anteile hat, ist eine Dramödie“. Diesen Satz formalisieren wir mit der Variable P. Es gibt jetzt nur P oder -P, aber nichts anderes. Es kann kein halbes Minus vor P geben. Gut, in diesem Fall gibt es sogar nur -P und alles andere ist falsch, liebe Kulturpessimist*innen.
Bevor jetzt der eine Logik-Nerd da hinten rechts aufschreit, dass meine Erklärung verkürzt war, hier einmal die richtige formallogische Notation für den Satz vom ausgeschlossenen Dritten:
¬(P∧¬P)
So, jetzt habt ihr das einmal gesehen/gehört und wir können mit dem wichtigen Kram weitermachen!
Einschränkungen des Satzes vom ausgeschlossenen Dritten
Wichtig sind jetzt schon die Einschränkungen. Wenn du den Satzes vom ausgeschlossen Dritten verstehen willst, musst du wissen, dass Aristoteles von der Satzebene ausgeht. In meiner Formalisierung eben stand P genau für einen Satz. Nicht für mehr und nicht für weniger. Wir sahen bereits in der Folge über die Kategorien, dass es eine wichtige Erkenntnis von Ari war, festzustellen, dass wahr oder falsch nicht einzelne Worte sind, sondern Sätze.
Er schränkt das aber sogar noch weiter ein, denn nicht alle Sätze kommen in Frage, wenn wir sie auf Wahrheit hin prüfen. Genau wie nicht alle Twitter*innen lustig sind. Ja, Ulf, ich meine dich! Deine Tweets sind nicht lustig! Wahr oder falsch können nur faktische, konstatierende Sätzen sein. Zudem müssen wir noch Ceteris paribus beachten. Okay, okay, das hier wird jetzt eine Orgie von Technobabble – ganz als würden Data und Geordi miteinander Smalltalken. Ich mache euch wieder an Beispielen deutlich, was ich meine:
„Auf YouTube gibt es Videos zu Philosophie“. Dieser Satz ist wahr oder falsch, aber nichts drittes. Rosenkohl ist lecker – wahr oder falsch. Nichts drittes. Na gut, manche von euch schreien jetzt vielleicht als hätte Edvard Munch euch gemalt, dass Rosenkohl auch ein bisschen lecker sein kann. Denn hier beim letzten Satz hat sich schon wieder eine Wertung eingeschlichen, es ist kein faktischer Satz. Lasst mich daher mit einem ganz berühmten Beispiel von G. E. Moore, das ihr auch bei Wittgenstein wiederfindet, aufzeigen, welche Art von Sätzen wir auf Wahrheit prüfen können.
Wenn wir einen Satz betrachten, der eine Tatsache über die Welt aussagt, dann ist dieser wahr oder falsch und nichts dazwischen. „Hier ist eine Hand.“ kann wahr oder falsch sein. Aber es kann hier nicht nur ein bisschen eine Hand sein und ein bisschen nicht. „Hier ist eine Hand“ ist ein konstatierender Satz, denn er macht eine Aussage über die Welt. Er stellt etwas fest. Würde unser Satz lauten „Ist hier eine Hand?“, dann könnten wir ihn nicht auf Wahrheit prüfen. Klar, oder?
Erst als ich jetzt die Stelle in De Interpretatione las, in der sich Ari fragt, welche Art von Sätzen wahr oder falsch sein können, fiel es mir wie Gurkenscheiben von den Augen in den Gin, dass John L. Austin sich auf diese Stelle in seiner Theorie der Sprechakte bezieht.
Austin schreibt am Anfang der Theorie der Sprechakte, dass die Performativa (wie er sie nennt), also Sprechakte, mit denen man Handlungen vollzieht, wie Fragen, Bitten und so, zwar schon anderen aufgefallen sind, ihnen aber nicht die angemessene Beachtung geschenkt wurde. Ich zitiere:
„Die Erscheinung, um die es geht, ist sehr weit verbreitet und liegt offen zutage; hier und da müssen sie andere bemerkt haben. Aber ich habe noch niemanden gefunden, der sich richtig darum gekümmert hätte.“
John L. Austin: Zur Theorie der Sprechakte*
Das bezieht sich, wenn man Austins subtilen Humor kennt, klar auf Aristoteles, der in De Interpretatione schreibt, dass beispielsweise Bitten keinen Wahrheitswert haben, das jetzt aber nichts zur Sache tue, er sich nicht darum kümmern werde und sich stattdessen nur auf Aussagen konzentrieren werde. Halten wir also fest: Wahr oder falsch sein, können also nur Aussagesätze oder Konstativa, wie Austin sie nennt. Sätze, die eine Tatsache konstatieren.
Ferner können (mehr oder weniger) nur faktische Sätze wahr oder falsch sein. Ein faktischer Satz sagt aus, dass etwas ist. Würden wir nur die Möglichkeit formulieren: „Hier könnte eine Hand sein.“, würde es mit der Wahrheitsprüfung schon schwieriger werden. Nicht unmöglich, aber komplizierter.
Zu guter Letzt müssen wir auch noch dieses komische Ceteris paribus beachten. Ceteris paribus klingt wie ein Zauberspruch bei Harry Potter, ist aber überraschenderweise Latein und bedeutet „unter sonst gleichen Bedingungen“. Es darf also keine Faktoren geben, die unmöglich machen „Hier ist eine Hand“ auf Wahrheit zu prüfen. Wenn ich beispielsweise das Licht ausschalte und dann sage „Hier ist eine Hand“, lässt sich nicht prüfen, ob der Satz wahr oder falsch ist.
Funfact: diesen kleinen logischen Zauberspruch habe ich auch erst vor kurzem gelernt zu benennen, als meine Haus- und Hof-Psychologin ihrer Disziplin untreu wurde, als wäre die Psychologie Mr. Chow und mir Searles Versuch vortrug, aus einem Sein auf ein Sollen zu schließen. Aber das ist eine andere Geschichte und soll ein anderes Mal erzählt werden.
Der Satz vom ausgeschlossenen Dritten ist jedenfalls eine der wichtigsten und grundlegendsten Wahrheiten, die wir kennen. Habermas spricht ein paar Jahrtausende später vom zwanglosen Zwang des besseren Arguments, das Vernunft und kommunikatives Handeln überhaupt erst ermöglicht. Wenn wir nicht akzeptieren, dass Sätze entweder wahr oder falsch sind, dann verliert das bessere Argument seinen zwanglosen Zwang. Konzepte wie Fakenews, „Alternative Facts“ und Verschwörungsmythen versuchen den Satz vom ausgeschlossenen Dritten aufzuweichen, indem sie behaupten, es gäbe nicht bloß bei Wert- und Geschmacksurteilen mehr als eine wahre Meinung, sondern auch bei Fakten. Aber das ist, wie wir bei Aristoteles lernen, falsch.
Werturteile und Geschmacksurteile
Unsicher erscheint uns der Satz vom ausgeschlossenen Dritten nämlich nur dann, wenn wir Wert- oder Geschmacksurteile äußern. „Bibi und Tina ist eine schlechte Fernsehsendung“ ist fraglos wahr, aber irgendwie nicht auf die gleiche Weise wie „Hier ist eine Hand“. Der Grund dafür ist, dass dieser Satz extrem voraussetzungsreich ist. Extrem viele andere Sätze muss ich als gegeben annehmen, um diesen einen Satz auf seine Wahrheit hin zu prüfen. Zum Beispiel: Es gibt objektiv ästhetisch Gutes. Oder: Die unkritische Darstellung von Klassenunterschieden als unhinterfragte Normalität ist schlecht. Es ist eben kompliziert.
Ich möchte nicht unerwähnt lassen, dass es höherwertige Logiken gibt, in denen der Satz vom ausgeschlossenen Dritten vertrackter wird als Aristoteles sich das dachte. Die Fuzzy Logic zum Beispiel beschäftigt sich mit Problemen wie diesem: An Straßen finden sich oft Schilder, die aussagen: Bei Nässe darf nur 80 km/h gefahren werden. Die Frage hier ist: Wie nass muss die Straße sein, damit die Regel gilt? Gilt sie schon, wenn nur ein einziger Tropfen auf den Asphalt fällt? Wann ist eine Straße eigentlich nass? Die Fuzzy Logic löst diese Art von Problemen so, dass sie nicht nur die Wahrheitswerte 1 = wahr und 0 = falsch annimmt, sondern mit graduellen Abstufungen arbeitet. Dann kann eine Straße eben zu 0,7 nass sein. Aber das ist auch eine andere Geschichte und soll ein anderes Mal erzählt werden.
Die Existenzbedingung
Kehren wir zu Ari zurück, denn der macht eine weitere wichtige Regel auf: Um zu beurteilen, ob ein Satz wahr oder falsch ist, muss das Subjekt existieren. „Sören Eddie Johanna von und zu Bibiundtinaingen ist 1,80 Meter groß.“ lässt sich nur auf Wahrheit hin prüfen, wenn ein Ding namens Sören Eddie Johanna von und zu Bibiundtinaingen existiert. Erneut lässt sich das formalisieren (was Ari allerdings noch nicht macht):
Es existiert ein x Für x gilt: Es ist Sören Eddie Johanna von und zu Bibiundtinaingen und es ist 1,80m groß ∃x x (Sören Eddie Johanna von und zu Bibiundtinaingen) ∧ (1,80m groß)
Das stellt uns natürlich vor das Problem, ob wir sagen können, dass der Satz „Einhörner haben genau ein Horn“ wahr ist. Er scheint wahr zu sein, aber nach Ari lässt er sich nicht auf Wahrheit hin prüfen, da Einhörner nicht existieren. Ja, ich weiß, das ist ein Schock. Aber irgendjemand musste es mal sagen. Dass ich Einhörnern Eigenschaften zuschreiben kann, diese aber logisch nicht auf Wahrheit prüfen, sollte sehr viel später Willard Van Orman Quine viele Kopfschmerzen bereiten. Da soll noch einmal jemand sagen, Philosophie habe keinen praktischen Nutzen! Eine von Robert Brandom inspirierte Auflösung könnte übrigens sein, dass sich die Wahrheit von „Einhörner haben genau ein Horn“ aus unserem Sprachgebrauch ergibt, indem wir uns nicht auf ein Ding in der Welt beziehen, sondern auf das, was wir aus Literatur gelernt haben. Aber das ist jetzt wirklich eine andere Geschichte und soll ein anderes Mal erzählt werden.
Die Kontradiktion
Unser nächster Abschnitt führt uns nun endlich zum angekündigten logischen Quadrat: Ari stellt fest, dass alles, was sich bejahen lässt auch verneinen lässt. Es gibt also zu jeder Aussage genau eine Negation dieser Aussage. Das folgt aus dem Satz vom ausgeschlossenen Dritten. Ich kann jeden Satz durch „nicht“ in seine Negation umwandeln:
„Es macht mehr Mühe eine Knoblauchpresse zu reinigen, als es Mühe macht, den Knoblauch gleich mit einem Messer zu hacken“. Lässt sich in „Es macht nicht mehr Mühe eine Knoblauchpresse zu reinigen, als es Mühe macht, den Knoblauch gleich mit einem Messer zu hacken“ umwandeln.
Die Aussage und ihre Negation schließen sich gegenseitig aus. Marlene Dietrich war entweder die Hauptdarstellerin in ‚Der Blaue Engel‘ oder sie war es nicht. Beides gleichzeitig ist nicht möglich. Wir sagen dazu: Die Negation einer Aussage ist ihre Kontradiktion. Nachdem wir nun „kontradiktorisch“ abgehakt haben, können wir uns „konträr“ widmen.
Das konträre Gegenteil
Denn die Kontradiktion scheint zu implizieren, dass es keine zwei verschiedenen Negationen zu einer Aussage geben kann. Klar, oder? Aber was ist mit: „Alle Menschen in Filmen sind Schauspieler*innen“. Diesen Satz kann ich doch auf zwei Arten verneinen: „Nicht alle Menschen in Filmen sind Schauspieler*innen“ und „Kein Mensch ins Filmen ist Schauspieler*in“. Da nenn mich einer 1 Pimmel! Haben wir etwa gerade den Satz vom ausgeschlossenen Dritten widerlegt?
Aristoteles sagt dazu, dass wir unterscheiden müssen zwischen Aussagen über Individuen, etwa Marlene Dietrich im Beispiel eben, und allgemeinen Aussagen. Etwa: Alle Schauspielerinnen. Später wurde diese Unterscheidung in der Logik noch weiter präzisiert. Demnach gibt es Existenzaussagen oder auch Partikularaussagen.
Es gibt ein X, dieses X ist Marlene Dietrich und dieses X ist die Schauspielerin in „Der blaue Engel. Auf der anderen Seite gibt es aber auch Allaussagen: Für alle x gilt, wenn sie in Filmen mitspielen, dann sind sie Schauspieler*innen.
Und beim letzten Fall können wir einerseits die Allaussage negieren. Also sagen, dass das Prädikat zwar ganz knorke ist, aber eben nicht auf alle X zutrifft, so wie das Metaverse möglicherweise eine gute Idee ist, aber äh … Nein, sorry, mir fällt kein Fall ein, indem Marcs – Oh, hi Marc – Metaverse eine Gute Idee ist …
Hingegen können wir durchaus zu dem Schluss kommen, dass nicht alle X in Filmen Schauspieler*innen sind. Andererseits können wir aber auch sagen, „wenn X in Filmen mitspielen, dann sind sie keine Schauspieler*innen. In diesem Fall sprechen wir noch immer über alle X, sagen aber diesmal, dass das Prädikat diesen X niemals nicht zugesprochen werden kann. Aristoteles nennt diesen letzten Fall das konträre Gegenteil.
Eine kleine Nebenbemerkung noch an dieser Stelle, um noch einmal die Metaphysik anzuteasern … Denn hier steckt noch ein weiterer Unterschied drin, der uns dann in der Metaphysik noch viele Schwierigkeiten machen wird: „Marlene Dietrich“ gehört zur Kategorie der Substanzen und sie ist ein Individuum. „Schauspielerin“ gehört ebenfalls zur Kategorie der Substanzen, aber es ist ein Gattungsbegriff in Aris Terminologie. Der Begriff bezeichnet also eine Gruppe von Individuen. Behaltet diese Unterscheidung schon einmal im Hinterkopf, denn sie wird noch sehr wichtig werden.
Halten wir für die Logik fest: Allaussagen oder allgemeine Aussagen in der Terminologie Aristoteles‘ haben sowohl ein konträres Gegenteil. Das konträre Gegenteil von „Mark Forster macht immer gute Musik“ – was offensichtlich falsch ist – ist: „Mark Forster macht nie gute Musik“
Diese Sätze haben aber auch eine Kontradiktion: Mark Forster macht nicht immer aber manchmal gute Musik. Nein, dieses Beispiel ist selbst den Philosoph*innen zu unrealistisch. Nehmen wir lieber:
Alle Menschen in Filmen sind Schauspieler*innen. Und Nicht alle Menschen in Filmen sind Schauspieler*innen.
Ein wichtiger Unterschied zwischen einer kontradiktorischen Beziehung und einer konträren ist, dass bei der Kontradiktion immer genau ein Satz wahr und ein Satz falsch sein muss. Während bei konträren Aussagen zwar nicht beide Sätze wahr sein können, wohl aber beide falsch. Um euch mit einem Standard-Beispiel der Philosophie zu quälen: Sowohl „Alle Schwäne sind weiß“, als auch „Kein Schwan ist weiß“ sind falsch, denn wahr ist „Einige Schwäne sind weiß“. Es müssen aber auch nicht beide Sätze falsch sein, wie das Mark-Forster-Beispiel gezeigt hast.
Allaussagen und Partikularaussagen
Schauen wir, was es noch für logische Relationen in diesem Quadrat gibt: Die Kontradiktion einer Allaussage ist immer die Negation einer Partikularaussage. Denn wenn es nur einen Menschen in Filmen gibt, der nicht Schauspieler ist, dann kann die Allaussage nicht wahr sein. Entsprechend ist die Kontradiktion zu:
Kein Mensch in Filmen ist Schauspieler*in. (Mindestens) Ein Mensch in Filmen ist Schauspieler*in.
Denn ein einziger Mensch reicht, damit die Aussage nicht wahr sein kann. Wie sieht es aus mit einer Partikularaussage und ihrer Negation? Da wir schon gelernt haben, dass es genau eine Kontradiktion gibt, können die beiden sich nicht ausschließen. Die Negation der Allaussage ist ja bereits die Kontradiktion der Partikularaussagen. Und genauso ist es auch! Beide sind wahr:
Einige Menschen sind Schauspieler*in. Einige Menschen sind nicht Schauspieler*in.
Die beiden Sätze sind kein Widerspruch, sie können sich ja auf verschiedene Menschen beziehen. Man nennt dieses Verhältnis auch subkonträr.
Hier sehen wir übrigens wieder diesen Unterschied bei den Substanzen, den ich nicht aufhöre, anzuteasern. Denn „Mensch“ war ja eine Substanz genau wie „Marlene Dietrich“. Aber Wir können nicht sagen, dass auch diese beiden Sätze wahr sind:
Marlene Dietrich ist Schauspielerin. Marlene Dietrich ist nicht Schauspielerin.
Es scheint also innerhalb von Substanzen einen großen Unterschied zu geben. So groß, dass wir uns fragen müssen, ob wirklich beide Kategorien der gleichen Art sin. Ich denke, wir sind hier etwas Großem auf der Spur … Grund genug also, um diese Spur fallen zu lassen und stattdessen zur Logik zurückzukehren. Und ich weiß, dass wird langsam so ermüdend wie ein Film von Terrence Malick. Aber Systematik war eben Aris ganz persönlicher Kink und Logik ohne Systematik ist Schmutz, also lasst es uns nach Hause bringen.
Das logische Quadrat
Das Ganze lässt sich jetzt in unser Quadrat packen, wie ich bereits in der Einleitung anteaserte, falls ihr euch noch daran erinnern könnt. Meine Folgen haben bald so viele Teaser wie der Abspann eines Marvel-Films. Falls ihr euch nicht mehr an das logische Quadrat erinnern könnt, kann ich es euch nicht verübeln, denn mir raucht auch der Kopf. Aber bleibt noch kurz dran, dann haben wir es geschafft: Wir haben Allaussagen und Partikularaussagen. Diese können wir bejahen oder verneinen.
A sind unsere Allaussagen I sind Partikularaussagen E sind die Negation der Allaussagen Und O die Negation der Partikularaussagen
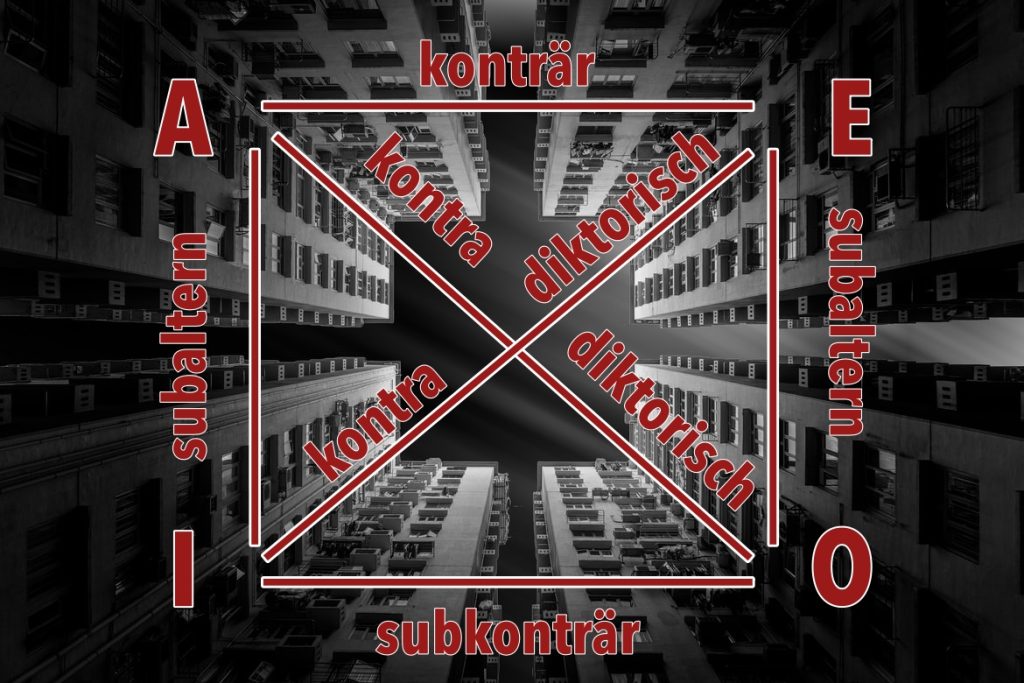
Konträr sind Allaussagen A und ihre Negation E:
Alle Tiktoker*innen sind laut und aufgekratzt. Kein*e Tiktoker*in ist laut und aufgekratzt.
Kontradiktorisch verhalten sich Allaussagen A und die Negation von Partikularaussagen O:
Alle Tiktoker*innen sind laut und aufgekratzt. Einige Tiktoker*innen sind nicht laut und aufgekratzt.
Sowie die Negation der Allaussagen E und die Partikularaussagen I:
Kein*e Tiktoker*in ist laut und aufgekratzt. Einige Tiktoker*innen sind laut und aufgekratzt.
Subkonträr sind Partikularaussagen I und ihre Negation O:
Einige Tiktoker*innen sind laut und aufgekratzt. Einige Tiktoker*innen sind nicht laut und aufgekratzt.
Schließlich gibt es noch das Verhältnis Subaltern (das ich bislang noch unerwähnt ließ). Das bedeutet, dass ein Satz einen anderen impliziert. Das also ein Satz schon in einem anderen steckt:
Alle Tiktoker*innen sind laut und aufgekratzt. Einige Tiktoker*innen sind laut und aufgekratzt.
Wenn die Allaussage wahr ist, dann ist notwendig auch die Partikularaussage wahr. Genauso verhält es sich mit der Negation:
Kein*e Tiktoker*in ist laut und aufgekratzt. Einige Tiktoker*innen sind nicht laut und aufgekratzt.
Beide sind wahr. Alter! Was für ein Hazzle. Ich wünschte ich könnte sagen, das war es jetzt mit dem Stress. Allein: This is just the beginning. Wir stehen erst ganz am Anfang der Logik! Doch damit machen wir beim nächsten Mal weiter. Jetzt haben wir uns erstmal ein Bier verdient! Das ist mal wieder so eine Folge bei der ich mich wundere, ob Leute bis zum Ende aufgepasst haben. Philosophie ist eben nicht immer fluffig und leicht, sondern kann auch anstrengend sein. Wenn ihr es also bis hier hin geschafft habt, dann postet doch mal ohne weitere Erklärung „Marlene Dietrich ist Tiktokerin“ in die Kommentare, damit wir die Crowd da draußen verwirren können …
Ich in den sozialen Medien
Philosophie-Videos
- Semantik & De Interpretatione
- Die Kategorien
- Gattung und Art
- Alle Philosophie-Folgen
- Wie das mit der Philosophie angefangen hat
Zur weiteren Recherche über Aristoteles
Aristoteles – Die Kategorien *
Aristoteles – De Interpretatione *
Bertrand Russell – Die Philosophie des Abendlandes *
Christof Rapp – Aristoteles *
Otfried Höffe – Aristoteles: Die Hauptwerke *
Eduard Zeller – Die Philosophie der Griechen: Zweiter Teil: Sokrates, Plato, Aristoteles *
*Das ist ein Affiliate-Link: Wenn ihr das Buch kauft, bekomme ich eine winzige Provision und freue mich.
