- Download:
- MP3 Audio16 MB
- MPEG-4 AAC Audio12 MB
Aristoteles – Der Logiker – Folge 10
Heute geht es um Logik. Das ist die Lehre vom richtigen Schließen. Wir schauen uns noch einmal an, was ein Schluss ist, was ein Beweis und worin der Unterschied liegt zwischen vollkommenen und unvollkommenen Schlüssen. Dann kommen wir endlich zum klassischen Syllogismus. Als nächstes schauen wir uns verschiedene Schlussformen an. Wir wenden dann unsere verschiedenen Modi Notwendigkeit, Faktizität, Möglichkeit und Unmöglichkeit auf die Schlussformen an. Das alles gibt es wahlweise als Video, Podcast oder Text.
Wollt ihr mich unterstützen? Dann gebt mir doch einen Kaffee aus! 🙂
Ich auf Social Media
Mehr Videos
- Die erste Analytik
- Semantik & De Interpretatione
- Das Problem der Zukunftsaussage
- Alle Philosophie-Folgen
- Wie das mit der Philosophie angefangen hat
Zur weiteren Recherche über Aristoteles
- Aristoteles – Die Kategorien *
- Aristoteles – De Interpretatione *
- Aristoteles – Erste Analytik *
- Bertrand Russell – Die Philosophie des Abendlandes *
- Christof Rapp – Aristoteles *
- Otfried Höffe – Aristoteles: Die Hauptwerke *
- Eduard Zeller – Die Philosophie der Griechen: Zweiter Teil: Sokrates, Plato, Aristoteles *
- Herman Siebeck – Aristoteles *
Aristoteles‘ Logik
Nach den vielen Vorüberlegungen zur Logik möchte ich heute schließlich mit der eigentlichen Lehre der Logik beginnen. Das ist die Lehre vom richtigen Schließen. Und damit dann auch den Logik-Block der Aristoteles-Staffel beenden und mich anderen Themen zuwenden. Ich bin also wie eine Folge von Amazons-Blockbuster-Serie Ringe der Macht: Lange geschieht nichts und kaum könnte der eigentliche Spaß beginnen, ist sie auch schon wieder vorbei.
Was euch erwartet
Wir schauen uns noch einmal an, was ein Schluss ist, was ein Beweis und worin der Unterschied liegt zwischen vollkommenen und unvollkommenen Schlüssen. Dann kommen wir endlich zum klassischen Syllogismus. Als nächstes schauen wir uns verschiedene Schlussformen an. Wir wenden dann unsere verschiedenen Modi Notwendigkeit, Faktizität, Möglichkeit und Unmöglichkeit auf die Schlussformen an.
Was ist ein Schluss?
Auch wenn wir das schon ein paarmal hatten, sollten wir dennoch ganz im Stile Aristoteles‘ uns systematisch fragen: Was ist das eigentlich – ein Schluss?
Kehren wir dafür zu unserer Definition aus der letzten Folge zur ersten Analytik zurück:
Aristoteles definierte den Schluss dort als eine Rede, bei der etwas als gegeben angenommen wird. So wie wir alle Jahrzehntelang als gegeben annahmen, dass unser Gas aus Russland kommt. Daraus folgt dann etwas anderes notwendig. Mein Teaser in der Folge zur ersten Analytik war: Wenn wir die beiden folgenden Sätze als gegeben annehmen
- dass politische Parteien das Grundgesetz akzeptieren müssen, um demokratische Parteien zu sein
- dass die AfD das Grundgesetz ablehnt
Dann folgt nach Ari daraus „etwas anderes“ notwendig. Was folgt, habe ich beim letzten Mal noch verschwiegen. Jetzt hole ich das nach Es folgt nämlich: „Die AfD ist keine demokratische Partei“. Und warum das der Fall ist, das klären wir heute!
Was ist ein Beweis?
Zu dieser Klärung ist wichtig, dass wir als nächstes Aristoteles Verwendung des Begriffs „Beweis“ abstecken. Aristoteles sagt in der ersten Analytik, dass ein Beweis eine Art des Schlusses ist, aber nicht jeder Schluss ist ein Beweis. So wie Elrond in Ringe der Macht ein Elb mit extrem schönen Haaren ist, aber nicht jeder Elb mit extrem schönen Haaren Elrond heißt. Was Aristoteles „Beweis“ nennt, nennen wir heute deduktiven Schluss: Der Schluss vom Allgemeinen zum Besonderen und unterscheiden das von anderen Schlussformen wie der Induktion, wo ich vom Besonderen zum Allgemeinen schließe.
Wie genau funktioniert denn dieser Beweis? Was macht ihn wahr? Um das zu beantworten, schlagen wir den langen Bogen zurück zur ersten inhaltlichen Folge dieser Staffel. Dort hatte ich erklärt, was Gattung und Art sind und ihr hattet euch vielleicht gefragt: Warum zum Grottenolm müssen wir uns das anhören?! Ganz einfach: Weil der Weg bei der Deduktion immer von der Gattung zur Art geht. Wenn ich sage, dass die Gattung ‚Auto mit Verbrennungsmotor‘ schlecht fürs Klima ist, dann trifft das auch auf die Auto-Art Porsche zu. Denn die Auto-Art Porsche ist per Definition in der Gattung ‚Auto mit Verbrennungsmotor‘ enthalten.
Vollkommener und unvollkommener Schluss
Wir unterscheiden weiter zwischen einem vollkommenen Schluss und einem unvollkommenen. Für einen vollkommenen Schluss brauchen wir nur einen Oberbegriff A, einen mittleren Begriff B und einen unteren C. Der untere muss ganz im mittleren sein und der mittlere ganz oder gar nicht im oberen.
Was Ari damit meint, dass ein Begriff in einem anderen enthalten ist, hatten wir beim letzten Mal ja schon. Es bedeutet, dass wir den Begriff so umformen können, dass der andere Begriff zum Vorschein kommt. Allerdings hatte ich das einfach so in den Raum gestellt und nicht erklärt, warum das so ist. Das geht ja nicht. Denn: Was sind wir? Philosophen! Und was wollen wir? Begründungen!
Und diese Begründung liefern uns eben die Begriffe „Gattung“ und „Art“. Wenn wir aus A und B auf C schließen wollen, dann muss jedes C Teil der Art B sein und jedes B oder keines (dazu kommen wir gleich) muss zur Gattung A gehören.
Mit einem Venn- Diagramm kann man das wieder schön veranschaulichen.
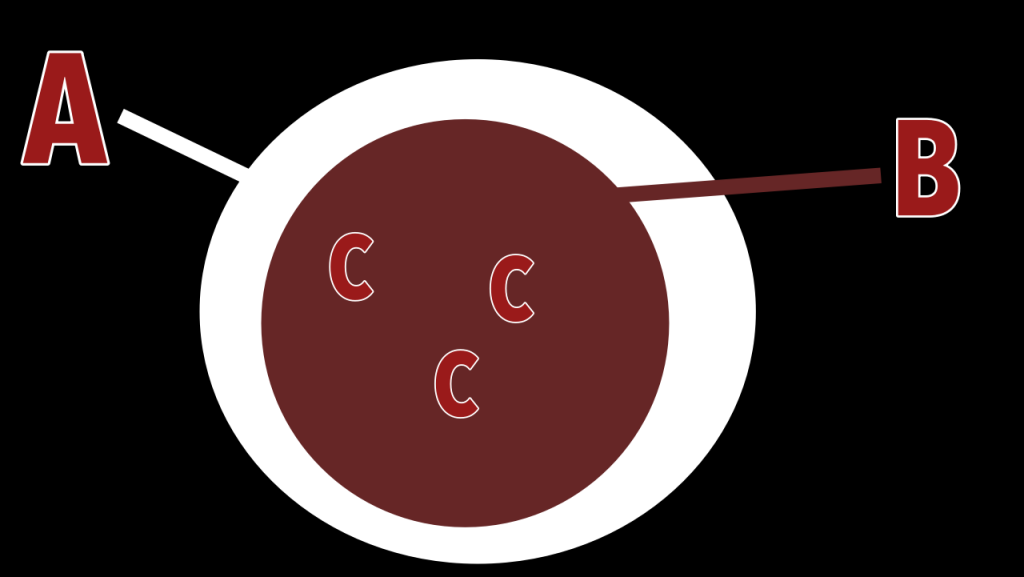
So können wir sagen, dass Elrond Art zur Gattung Elb mit schönen Haaren ist (lasst mir das zumindest vorläufig mal so durchgehen) und Elb mit schönen Haaren ist wieder Art zur Gattung Elb.
Als Terminus medius (also als B in unserer Begriffsreihe A, B, C) kann also nur ein Begriff fungieren, der einen anderen in sich trägt und der selbst in einem anderen getragen wird oder nicht (je nachdem, welchen Schluss wir daraus ziehen). Im Beispiel eben ist „Elb mit schönen Haaren“ unser Terminus Medius – auch wenn diese Haare alles andere als Medius sind, sondern nichts anderes als Primus!
Der klassische Syllogismus
Und damit kommen wir endlich zu dem, was wir den klassischen Syllogismus nennen: Wenn man A von allen B aussagen kann und B von allen C aussagen kann, dann folgt daraus, dass man A von allen C aussagen kann.
Wenn ich von allen Menschen (B) sagen kann, dass sie sterblich (A) sind und von allen Athenern (C), dass sie Menschen (B) sind, dann kann ich von allen Athener (C) sagen, dass sie sterblich (A) sind.
Okay, jetzt habt ihr euch vielleicht gefragt, warum ich das so kompliziert beschrieben und nicht einfach gesagt habe, dass alle A B sind und alle B sind C, sodass folgt, dass alle A C sind. Das liegt einfach an der Grammatik des Deutschen. An der Oberflächenstruktur sieht man da die logischen Klassen nicht so leicht. Mit einem Venn-Diagramm können wir aber wieder schön die logische Tiefenstruktur visualisieren.

Und damit ihr nicht immer nur das gleiche Beispiel hört, das alle unkreativen Philosoph*innen euch vor den Latz knallen, hier noch ein anderes. Denn schließlich ist der klassische Syllogismus ja nicht nur für diesen einen Satz wahr, sondern eben für alle, die die gleiche Form, die gleiche Tiefenstruktur haben.
Mikrotransaktionen sind dazu da, Gamer*innen das Geld aus der Tasche zu ziehen. Roblox finanziert sich über Mikrotransaktionen. Daraus folgt: Roblox ist dazu da, Gamer*innen das Geld aus der Tasche zu ziehen.
Diese Konklusion ist wahrscheinlich etwas kontroverser als jene, dass Athener sterblich sind. Wenn ihr jetzt hardcore Roblox-Fans seid und schreit „Das ist eine Lüge, Roblox ist total toll und zieht niemandem Geld aus der Tasche!!!“ Dann lautet meine Antwort darauf: 1. Mein Beileid. Und 2. Das ist ein zwingender Schluss, der notwendig aus den Prämissen folgt. Wenn du darlegen willst, dass es falsch ist, dass Roblox Gamer*innen das Geld aus der Tasche zieht, dann musst du eine der beiden Prämissen angreifen und darlegen, dass sie falsch sind.
Denn eines ist wichtig zu verstehen: Die Logik ermittelt Wahrheit nur aufgrund der Struktur der Sätze. Ob die Prämissen inhaltlich wahr sind, ist debattierbar, das müssen laut Aristoteles die Einzelwissenschaften zeigen. Die Logik kann nicht beweisen, dass Mikrotransaktionen wirklich Gamer*innen das Geld aus der Tasche ziehen. Hierzu müssen sich Ökonomie, Ethik und Politik äußern.
Verschiedene Schlussformen
Das ist also der klassische Syllogismus. Es ist ein vollkommener Schluss, der darauf aufbaut, dass wir mit zwei Allaussagen hantieren. Wie sieht es aus, wenn wir eine davon negieren, also verneinen? Damit kommen wir zu dem schon angesprochenen Fall, dass der mittlere Begriff gar nicht im oberen enthalten ist.
Wenn kein A B ist, aber alle B C, dann ist auch kein A C.
Wenn Kein Mensch fliegen kann und alle Athener Menschen sind, dann kann kein Athener fliegen.
Auch hier wieder ein zweites Beispiel:
Wenn kein Mensch ‚Moon Knight‘ gucken konnte, ohne einzuschlafen und alle Oscar-Isaac-Fans Menschen sind, dann konnte kein Oscar-Isaac-Fan ‚Moon Knight‘ gucken, ohne einzuschlafen.
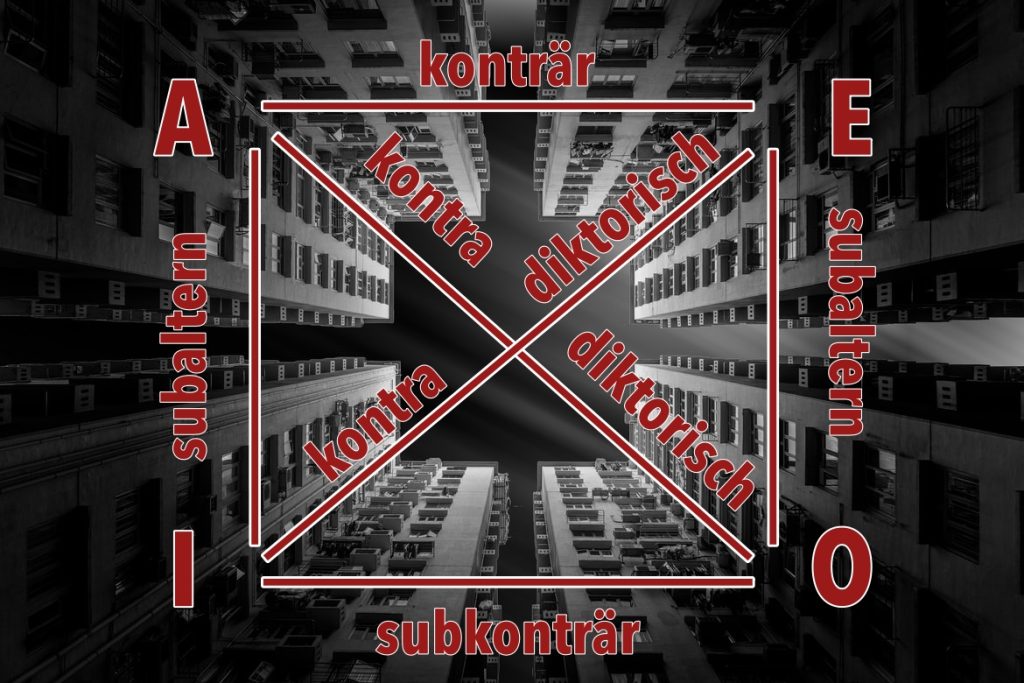
Im nächsten Schritt können wir jetzt die olle Tiktokerin Marlene Dietrich wieder rausholen und unser logisches Quadrat von neulich weiter durchgehen und eine der Allaussagen zu einer Partikular-Aussage machen.
Wenn von allen A B ausgesagt werden kann und von einigen B C ausgesagt werden kann, dann kann auch von einigen A C ausgesagt werden.
Das führt uns wahrscheinlich zum berühmtesten Beispiel der Philosophiegeschichte:
Wenn alle Menschen sterblich sind und Sokrates ein Mensch ist, dann ist Sokrates sterblich.
Auch bei dieser Schlussform gilt übrigens die Negation: Wenn A keinem B und B einigen C zukommt, dann kann A nicht von einigen C ausgesagt werden.
Wenn kein Mensch fliegen kann und Sokrates ein Mensch ist, dann kann Sokrates nicht fliegen.
Dazu drei Bemerkungen:
Wenn du jetzt nicht schon drei Jahrzehnte Philosophie-Milch geschlürft hast, sondern noch einigermaßen normal denken kannst, dann fragst du dich jetzt vielleicht: Wieso sagt der komische Honk erst „von einigen B kann C ausgesagt werden“, um dann als Beispiel zu bringen: Sokrates ist ein Mensch. Sokrates ist doch nicht Ygramul, die Viele aus der unendlichen Geschichte, sondern einer.
Und da habt ihr natürlich vollkommen recht! Ari unterscheidet manchmal auch zwischen Aussagen über einzelne Individuen und solchen über Gruppen. Aber rein logisch betrachtet macht es keinen Unterschied, ob Sokrates ein Individuum ist oder Teil des Borg-Kollektivs ist. Sokrates ist ein Erfüllungsgegenstand der Art Mensch. Ich hoffe, der alte Ironiker verzeiht mir, dass ich ihn Gegenstand nenne. Jedenfalls gilt für einen Erfüllungsgegenstand das Gleiche wie für eine Gruppe von 5, 50 oder 500. Solange es sich um eine Teilmenge der Gesamtmenge (hier der Gesamtmenge Menschen) handelt, solange kann ich mit einem Sokrates die gleichen Schlüsse ziehen wie mit einigen Sokratessen.
Wenn ich also sage „Wenn von allen A B ausgesagt werden kann und von einigen B C ausgesagt werden kann, dann kann auch von einigen A C ausgesagt werden.“, dann ist „Sokrates“ dieses Einige. Klingt komisch, ist aber so. Ich sage hier: Es gibt die Gattung Sterbliche, die Art Menschen und einen oder mehrere Erfüllungsgegenstände, die wir Sokrates nennen.
Das zweite, was es hier zu sagen gibt, ist, dass die Bedeutung der Variablen, die Aristoteles nutzt, nicht zu unterschätzen ist. Er ersetzt Begriffe durch A, B, C usw. Dies war ein erster Schritt in Richtung formaler Logik. Ein erster Schritt in Richtung der Verwendung von Codes und Algorithmen. Ohne diesen Schritt von Aristoteles vor 2200 Jahren wäre das Computerzeitalter nicht möglich. Du kannst gerade nur deshalb YouTube gucken, weil Ari im antiken Griechenland niederschrieb: Wenn alle A B sind und alle B C, dann sind alle A C. Und, ja, ich weiß, ich habe etwas ähnliches schon über Platons Sprachphilosophie gesagt. Doch das eine macht das andere nicht falsch! Platon hat sich nur theoretische Gedanken über eine Idealsprache gemacht, die zur Formalisierung führte. Aristoteles ist den ersten Schritt gegangen und allein dafür ist sein Status als Der Logiker, oder als der Philosoph, wie man ihn im Mittelalter nannte, absolut gerechtfertigt.
Der dritte Gedanke ist, dass an dieser Stelle Einführungen und Zusammenfassungen von Aris Logik oft schon enden. So wie die erste Staffel Ringe der Macht auch gerade dann endete, als wir gerade gelernt hatten, wer Sauron it. Wenn wir in den Text blicken – ich meine jetzt wieder die erste Analytik und nicht das Silmarillon, an dem wir ja auch keine Rechte haben –, dann befinden wir uns gerade auf Seite 7 der Prior Analytica. Was zur veganen Bolognese macht der Systematik-Freak auf den restlichen 141 Seiten?!
Das, was wir hier gerade gesehen haben, nennt Aristoteles vollkommene Schlüsse. Wir sprachen ja bereits darüber. Einen vollkommenen Schluss kann ich ziehen, ohne dass ich dafür irgendeine Zusatzannahme brauche. Hinzu kommen aber noch weitere, nicht vollkommene Schlüsse. Diese sind zwar auch logisch, aber ihre Wahrheit erschließt sich eben oft erst durch Zusatzannahmen und Umformungen.
Am Ende kommt Aristoteles auf drei Figuren von logischen Schlüssen mit vier bis sechs Untergruppen. Diese haben so ulkige Namen, als kämen sie direkt aus House of the Dragon. Sie heißen zum Beispiel Barbara, Ferio, Baroco oder Datisi. Allerdings hat Ari sie nicht selbst benannt, das geschah erst im Mittelalter im Zuge der Rezeption der Ersten Analytik.
Nachdem der olle Philosoph jetzt also die Schlussformen etabliert hat, kommt er um die Ecke mit: „Sodele, Kinners, jetzt kennen wir die Schlüsse, aber ich habe euch vorhin schon verklickert, dass Sätze notwendig, faktisch, möglich oder unmöglich sein können. Wie sehen denn unsere Schlüsse aus, wenn wir sie mit diesen verschiedenen Modi von Sätzen ziehen und wie, wenn wir diese Modi schön durchwürfeln?“ Anschließend fragt er sich noch, wie es zu so etwas wie Fehlschlüssen kommen kann.
Ich könnte jetzt jede einzelne Prüfung von möglichen Schlussfolgerungen mit euch durchgehen, aber dann könnte ich den Blog auch gleich dicht machen, denn niemand würde das durchstehen. Wenn ihr die Logik des Aristoteles lernen wollt, dann bleibt euch nichts anderes übrig, als in den Text zu gucken. Und ich empfehle jeder da draußen, Logik zu lernen. Aber mal Realtalk: Es gibt didaktisch bestimmt bessere Ansätze als die erste Analytik von Aristoteles.
Das ist schon allein deshalb der Fall, weil Ari nur die Syllogismen mit zwei Prämissen betrachtet, was nur eine kleine Auswahl aller möglichen Schlussfolgerungen ist. Ari glaubte, dass alle Argumente sich auf seine Schlussfolgerungen zurückzuführen ließen. Das war ein Irrtum, den bereits die Stoiker kritisierten.
Ich könnte jetzt hier Schluss machen mit meiner Staffel zu Aristoteles‘ Logik, aber eine kleine Extrarunde drehe ich noch. Denn mein Anspruch ist es, bewusst immer etwas tiefer in die Philosophie einzutauchen, als es 90 % der anderen hier machen. Daher will ich euch zumindest ein paar der anderen Schlussfolgerungen als Appetithäppchen hinwerfen. Ganz so als wäre ich Sam, ihr wäret Frodo und die Logik von Aristoteles wäre zugeworfenes Lembas.
Unvollkommene Schlüsse
Schauen wir uns zunächst einen unvollkommenen Schluss an:
M wird von keinem N aber von allen X ausgesagt. Daraus folgt, dass N keinem X zukommen kann. Der Schluss ist unvollkommen, da er zunächst umgeformt werden muss, um zeigen zu können, dass er wahr ist. Hier kommt die Regel zum Einsatz, die wir beim letzten Mal kennengelernt haben, dass eine allgemeine Verneinung allgemein konvertibel ist. Wenn M keinem N zukommt, dann kommt auch N keinem M zu. Dann haben wir den Schluss kein N ist M und alle M sind X, daraus folgt, dass kein N X ist. Warum zum Lower-Decks-Red-Shirt musste ich mir eigentlich ausgerechnet die beiden Variablen auswählen, die sich akustisch am schwersten unterscheiden lassen?
Nehmen wir daher schnell ein Beispiel, um das anschaulicher zu machen:
Die Erdenschwerkraft kann kein Gürtler und jedes UN-Mitglied aushalten. Das können wir umformen in kein Gürtler kann Erdenschwerkraft aushalten, aber jedes UN-Mitglied kann Erdenschwerkraft aushalten. Damit ist Erdenschwerkraft zum mittleren Term geworden und wir können folgern, dass kein Gürtler UN-Mitglied ist. Was wir gemacht haben, ist nämlich, dass wir aus dem unvollkommenen Schluss durch die Umformung wieder einen vollkommenen Schluss gemacht haben. Yeah!
Die Modalitäten
So, bald haben wir es, aber uns fehlen noch die Modalitäten. Ihr erinnert euch: Nach Ari kann ein Satz notwendig wahr sein, faktisch wahr sein oder es kann die Möglichkeit bestehen, dass er wahr ist. Je nachdem, an welcher Position in meinem Syllogismus welcher Modus steht, folgt daraus unterschiedliches. So wie Unterschiedliches aus den hohen Gaspreisen folgt, je nachdem, welche Zahl auf deinem Kontoauszug steht.
Wenn der Obersatz allgemein und notwendig ist, dann wird auch der Schluss notwendig sein, stellt Aristoteles fest. Wenn A notwendig allen B zukommt und B faktisch einem C. Dann wird A notwendig einem C zukommen. Alle Menschen, die mit Corona infiziert sind, sind notwendig krank. Wenn ein hustender Mensch faktisch mit Corona infiziert ist, dann ist er notwendig krank. Das gleiche gilt für die notwendige Negation des Obersatzes.
Wenn A aber nur faktisch B zukommt, B hingegen notwendig C, dann ergibt sich daraus kein notwendiger Schluss. Denn dann besteht die Möglichkeit, dass A keinem C zukommt, selbst wenn es faktisch so ist. Also: Alle kranken Menschen sind faktisch mit Corona infiziert. Und ein kranker Mensch hustet notwendig, dann ist ein hustender Mensch in diesem Fall zwar faktisch mit Corona infiziert, aber nicht notwendig. Übrigens folgt auch aus dem Herbst, dass wir wieder alle Masken tragen solltet, um unser Gesundheitssystem zu entlasten.
Okay, wie sieht das mit der Möglichkeit oder wie man sie auch nennt: mit der Kontingenz aus?
Etwas ist möglich, stellt Ari fest, wenn es weder notwendig noch unmöglich ist. Eine spannende Eigenschaft der Kontingenz ist, dass sie sich im Gegensatz zur Notwendigkeit und Unmöglichkeit umkehren lässt und noch immer war ist: ‚Es ist möglich, dass X‘ und ‚Es ist möglich, dass nicht X‘ können beide gleichzeitig wahr sein. Bei ‚Es ist notwendig dass X‘ oder ‚Es ist unmöglich, dass x‘, trifft das nicht zu.
Ari präzisiert noch einmal, dass zwei Verwendungen von ‚Kontingenz‘ gibt und hebt damit den Widerspruch auf, der sich aus den verschiedenen Verwendungen in De Interpretatione und zu Beginn der ersten Analytik ergab. Wir nennen etwas kontingent, wenn es faktisch sein kann, aber nicht notwendig ist oder unmöglich. In dieser Verwendungsweise ist es kontingent, dass Deutschland zu Beginn des 21. Jahrhunderts eine Demokratie ist. Es ist aber unmöglich, dass Deutschland von einem Drachen regiert wird. Allerdings es ist notwendig, dass Deutschland (sofern es existiert) ein Land ist.
In der zweiten Verwendungsweise von Kontingenz meint sie: Etwas kann die Möglichkeit besitzen, etwas zu sein. Ohne das schon faktisch zu sein. Die FDP hat die Möglichkeit, im Niedersächsischen Landtag zu sitzen, tut es aber nicht. Okay, zutreffender ist vielleicht: Das Samenkorn hat die Möglichkeit, ein Baum zu werden, ist dies aber faktisch noch nicht. Merkt euch das, wir kommen im Zuge der Metaphysik darauf zurück.
Wir können jetzt alle Schlüsse, die wir kennengelernt haben, auch mit einer möglichen und einer faktischen Prämisse ziehen. Wenn eine Prämisse faktisch und die andere möglich ist, folgt daraus immer ein Schluss der Möglichkeit. Genauso verhält es sich bei einer notwendigen und einer möglichen Prämisse. Wenn alle Sessel notwendig Sitzgelegenheiten sind. Und einige Sessel möglicherweise blau sind. Dann sind einige Sitzgelegenheiten möglicherweise blau.
So, jetzt habe ich euch aber wirklich genug gelangweilt. Es ist an der Zeit die Logik hinter uns zu lassen. Wärt ihr Student*innen des Mittelalters, hättet ihr jetzt quasi das Grundstudium absolviert, einen Bachelor in Philosophie erworben. Jetzt haben wir das Handwerkszeug gelernt, um uns wirklich mit den Inhaltlichen Fragen der Philosophie zu beschäftigen. Doch bevor wir uns der erhabensten und abgehobensten aller philosophischen Disziplinen, der Metaphysik zuwenden, machen wir erst einmal eine kleine Pause von Aristoteles und beschäftigen uns beim nächsten Mal mit jemand anderem. Ihr dürft gespannt bleiben.
Doch halt! Bevor ihr geht, habe ich noch eine letzte Schlussfolgerung für euch:
Wenn alle Philosophie-Interessierten gerne richtig gute Videos auf YouTube schauen und die Abonnent*innen meines YouTube-Kanals regelmäßig richtig gute Videos gezeigt bekommen, dann sollten alle Philosophie-Interessierten meinen Kanal abonnieren.
Na, wer findet den Fehler?
*Das ist ein Affiliate-Link: Wenn ihr das Buch kauft, bekomme ich eine winzige Provision und freue mich.